Si bien es relativamente sencillo hacer una lista de algunos de los descubrimientos científicos más relevantes de la historia, del siglo o de la última década, establecer cuáles son los descubrimientos matemáticos que han marcado un antes y un después puede ser tarea algo más complicada.
Las Matemáticas han evolucionado desde sus orígenes de una manera muy fluida y constante, con cientos de matemáticos aportando nuevas ideas, nuevos conceptos y demostraciones, manteniendo comunicación entre ellos e intercambiando opiniones. Quizá una nueva idea era en realidad desarrollada durante 50 años por otros predecesores y demostrada al cabo de 100 años, con lo que establecer una fecha o un acontecimiento concretos podría resultar, además de falso, injusto para todos los que aportaron su conocimiento y dedicación.
A pesar de todo ello, hemos intentado hacer una selección de algunas de las bases fundamentales de las Matemáticas, que sirvieron para poder desarrollar posteriormente grandes ramas nunca antes imaginadas.
1. Teorema de Pitágoras
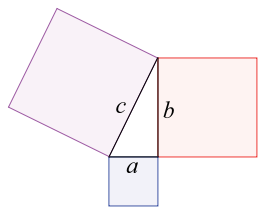
Establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Este teorema, junto con otros de Euclides (aprox. 365-300 a.C.), presentados en su obra «Elementos de Geometría» representan la base de la trigonometría, de gran aplicación hoy en día en medidas modernas y equipos tecnológicos.
2. Teorema fundamental del Cálculo
Gracias al desarrollo, a partir de la geometría analítica, de un nuevo enfoque geométrico y analítico de las derivadas matemáticas aplicadas sobre curvas definidas a través de ecuaciones y de una nueva notación matemática, Isaac Newton y Gottfried Leibniz crearon, en el siglo XVII, el cálculo infinitesimal, con lo que se inaugura la era del Análisis Matemático, la derivada, la integración y las ecuaciones diferenciales.
El teorema consiste en la afirmación de que la derivación e integración de una función son operaciones inversas. Esto significa que toda función continua integrable verifica que la derivada de su integral es igual a ella misma.
3. Euler

Leonhard Euler fue un matemático y físico suizo, considerado uno de los más grandes matemáticos de todos los tiempos. Una de sus principales contribuciones es la introducción de la notación matemática, incluyendo el concepto de función (y cómo la representamos con f(x)), funciones trigonométricas, la letra e, denominada constante de Euler, como base del algoritmo neperiano, la letra griega sigma ∑ para los sumatorios y la letra i para los números imaginarios, así como el símbolo π (pi) para la relación entre la longitud de una circunferencia y su diámetro. Además, estableció las reglas de utilización de los infinitos pequeños y desarrolló métodos de integración y de resolución de ecuaciones diferenciales.
4. Probabilidad
La doctrina de las probabilidades data de la correspondencia de Pierre de Fermat y Blaise Pascal (1654), si bien Christiaan Huygens (1657) le dio el tratamiento científico. Finalmente fueron Jakob Bernoulli y Abraham de Moivre quienes trataron el tema como una rama de las matemáticas.
Gracias a la Probabilidad se pueden extraer conclusiones sobre la probabilidad discreta de sucesos potenciales y la mecánica subyacente discreta de sistemas complejos en áreas como la estadística, la física, la matemática y la filosofía.
5. Teorema del valor medio
Demostrado por Joseph-Louis Lagrange (1736-1813), este teorema es una propiedad de las funciones derivables en un intervalo. Algunos matemáticos consideran que este teorema es el más importante de cálculo y se usa normalmente para demostrar otros teoremas.

Viñeta del ilustrador cómico Montt
6. Teorema fundamental de la Aritmética
Afirma que todo entero positivo se puede representar de forma única como producto de factores primos. Prácticamente demostrado por primera vez por Euclides, su primera demostración completa apareció de la mano del genio Carl Friedrich Gauss, en 1801.
7. Teorema fundamental del Álgebra
Establece que todo polinomio de una variable no constante con coeficientes complejos tiene una raíz compleja. Después de varios intentos por parte de Euler, Foncenex, Lagrange, Laplace y Gauss entre otros por demostrar este teorema, fue Jean-Robert Argand quien en 1806 publicó una prueba correcta para el teorema, enunciando el teorema fundamental del álgebra para polinomios con coeficientes complejos.
8. Concepto de espacio vectorial
En álgebra abstracta, un espacio vectorial es una estructura algebraica creada a partir de un conjunto no vacío, una operación interna y una operación externa, con 8 propiedades fundamentales. A los elementos de un espacio vectorial se les llama vectores.
A partir del concepto de espacio vectorial y sus implicaciones, se desarrolló una parte del álgebra de importantes aplicaciones en otras ramas de la matemática, la ciencia y la ingeniería, como por ejemplo las rutinas modernas de compresión de imágenes y sonido.
9. Álgebra de Boole
También llamada álgebra booleana, es una estructura algebraica que esquematiza las operaciones lógicas Y, O, NO y SI (AND, OR, NOT, IF), así como el conjunto de operaciones unión, intersección y complemento, utilizando únicamente los números 0 y 1.
Definida por el matemático inglés George Boole en 1847, el álgebra de Boole supone el punto de partida para la lógica matemática y base de la electrónica digital.
10. Teoría de Juegos
En 1928, el matemático John von Neumann desarrolla de manera amplia lo que anteriormente se había planteado como análisis de estrategia y teoría de juegos, convirtiendo la teoría de juegos en campo de estudio propiamente. La teoría de juegos utiliza modelos para estudiar interacciones en estructuras formalizadas de incentivos (los llamados «juegos») y llevar a cabo procesos de decisión, estudiando las estrategias óptimas así como el comportamiento previsto y observado de los individuos en juego. Desarrollada en sus comienzos como una herramienta para entender el comportamiento de la economía, la teoría de juegos se usa actualmente en muchos campos, como en biología, sociología, psicología y filosofía.















